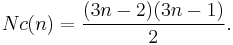Centered nonagonal number

A centered nonagonal number is a centered figurate number that represents a nonagon with a dot in the center and all other dots surrounding the center dot in successive nonagonal layers. The centered nonagonal number for n is given by the formula

$Nc(n) = \frac{(3n-2)(3n-1)}{2}.$

Multiplying the (n - 1)th triangular number by 9 and then adding 1 yields the nth centered nonagonal number, but centered nonagonal numbers have an even simpler relation to triangular numbers: every third triangular number is also a centered nonagonal number.

Thus, the first few centered nonagonal numbers are

1, 10, 28, 55, 91, 136, 190, 253, 325, 406, 496, 595, 703, 820, 946.

Note the following perfect numbers that are in the list:

The 3rd centered nonagonal number is 7 x 8 / 2 = 28, and the 11th is 31 x 32 / 2 = 496.

Proceeding further: the 43rd is 127 x 128 / 2 = 8128, and the 2731st is 8191 x 8192 / 2 = 33,550,336.

Except for 6, all even perfect numbers are also centered nonagonal numbers, with formula

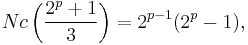$Nc\left(\frac{2^p%2B1}{3}\right) = 2^{p-1}(2^p-1),$ where 2^p-1 is a Mersenne prime.

In 1850, Pollock claimed (without proof) that every natural number is the sum of at most eleven centered nonagonal numbers, a conjecture which has been neither proven nor disproven.

Centered nonagonal number

See also